在某些應用中，若整個時間范圍內作用于系統(tǒng)的凈加速或力是重力，那么可以使用加速度計來測量傾斜的靜態(tài)角度。這類應用有：游戲機、相機中的水平檢測，以及在工業(yè)和醫(yī)療應用中檢測設備的駛向。

 

對于采用加速度計的傾斜檢測，假設重力是唯一的加速激勵因素。在實際使用中，可在信號輸出端執(zhí)行信號處理，移除輸出信號的高頻成分，因此一定程度的交流加速度是可以接受的。

 

傾斜檢測利用重力矢量及其在加速度計軸上的投影來確定傾斜角度。由于重力是直流加速度，任何產生額外直流加速度的力均會破壞輸出信號，導致計算錯誤。直流加速度的來源包括車輛在一定時間內以恒定速度加速，以及旋轉器件在加速度計上產生向心加速度。此外，通過重力旋轉加速度計，隨著目標軸上的重力投影變化，會引起明顯的交流加速度。在計算傾斜之前，對加速度信號進行任何形式的濾波都會影響建立輸出新靜態(tài)值的速度。

 

本應用筆記討論將加速度計輸出轉換為傾斜角度的基本原理。討論內容包括如何計算單軸、雙軸或三軸解決方案的理想傾斜角度。此外還包括一些關于校準的基本信息，以減少失調和靈敏度失配所引起的誤差。

 

傾斜計算

 

單軸傾斜計算

 

在只需對有限的角度范圍內進行傾斜檢測的應用中(該應用的分辨率精度較低)，可使用單軸器件(或多軸器件中的單個軸)。

 

例如，在圖1中，單軸(本例中是x軸)通過重力旋轉。由于此方法僅使用單軸，且需要重力矢量，因此只有當器件的x軸始終位于重力平面上時，傾斜計算角度才是精確的。其他軸上的任何旋轉都會降低加速度在x軸上的幅度，計算傾斜角度時便會產生誤差。

 

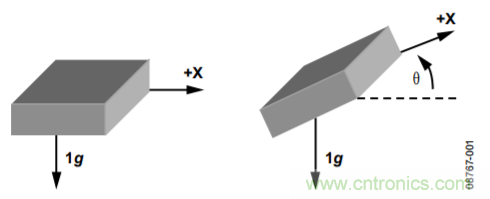
圖1. 用于傾斜檢測的單軸

 

根據(jù)基本三角恒等式，x軸上的重力矢量投影會產生輸出加速度，大小等于加速度計x軸和水平面之間夾角的正弦值。水平面通常是與重力矢量正交的平面。當重力為理想值1 g時，輸出加速度為：

 

 

使用單軸解決方案時——也就是說，輸出的變化引起輸入的某些變化——傾斜計算隨著水平面與x軸夾角的增加而下降，當夾角接近±90°時，數(shù)值接近0。這點可以從圖2中看出，其中繪出了輸出加速度(以g表示)與傾斜角之間的關系圖。接近±90°時，傾斜角出現(xiàn)很大變化時，輸出加速度只會產生很小變化。

 

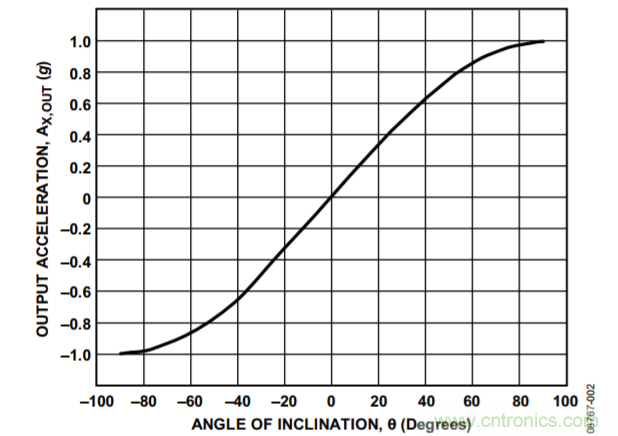
圖2. 輸出加速度與傾角的關系(單軸傾斜檢測)

 

由于以數(shù)字化的方式執(zhí)行傾斜計算，輸出加速度根據(jù)最低有效位(LSB)或代碼表現(xiàn)為恒定加速度，并由模數(shù)轉換器(ADC)獲取，或者直接從數(shù)字輸出部分獲取。由于輸出分辨率是恒定的加速度，傾斜分辨率(以度為單位)是可變的，其最佳分辨率接近0°，最差分辨率為±90°。

 

圖3和圖4顯示傾角步進為1°和0.25°時的增量靈敏度。增量靈敏度等于輸出變化，以mg顯示，表示每個傾角的步進，或者：

 

 

其中：

 

N為當前角度。

 

P為步長。

 

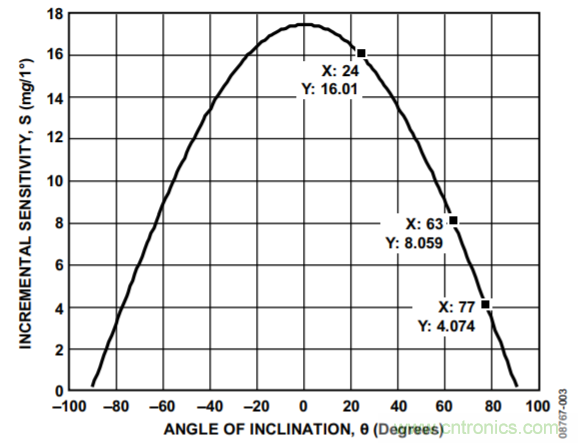
圖3. 步進為1°時的增量傾斜靈敏度

 

圖4. 步進為0.25°時的增量傾斜靈敏度

 

測量輸出加速度時，為了滿足應用在整個范圍內所需的傾斜分辨率，可利用這些曲線確定需達到的最小分辨率。例如，設計最大步長為1°，則針對±63°范圍，分辨率至少需達到8 mg/LSB。類似地，為達到±63范圍內的0.25°最大步長，則分辨率至少為2 mg/LSB。請注意，如果存在較大的擾動，可以使用過采樣以獲得更佳分辨率。

 

通過重力旋轉時，由于加速度計輸出符合正弦關系，使用反正弦函數(shù)可以將加速度轉換為角度。

 

 

其中，傾斜角θ單位為弧度。

 

如果需要窄范圍傾斜，可以使用線性近似法取代反正弦函數(shù)。線性近似與小角度正弦近似有關。

 

 

其中，傾斜角θ單位為弧度。

 

額外的比例系數(shù)k可用于傾角的線性近似計算中，若容許的誤差有所增加則可擴大近似的有效范圍。

 

 

其中，傾斜角θ單位為弧度。

 

將等式5的結果乘以(180/π)，可轉換為度。圖5顯示使用反正弦函數(shù)與使用k = 1時線性近似的對比。隨著傾角幅度的增加，線性近似開始下降，計算得到的角度與實際角度發(fā)生偏差。

 

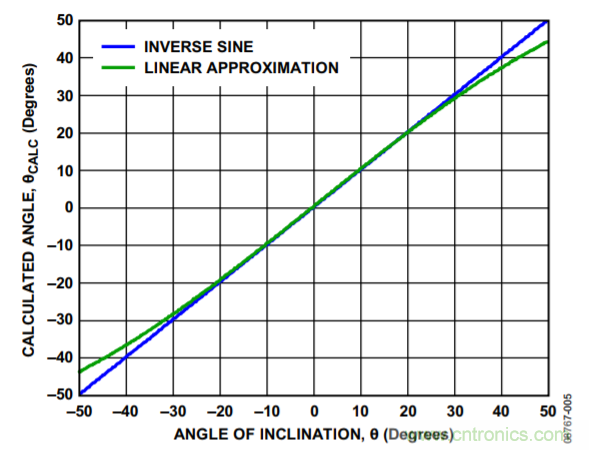
圖5. 傾角計算中反正弦函數(shù)與線性近似的對比

 

由于計算角度根據(jù)實際傾角繪制，因此線性近似在靠近尾部時開始彎曲。這是因為線性近似僅在對比輸出加速度時才表現(xiàn)為線性，如圖2所示。隨著傾角增加，輸出加速度的表現(xiàn)與之相似。然而，反正弦函數(shù)應當產生與實際傾角一對一對應的輸出，從而當描繪實際傾角時，計算得到的角度為一條直線。

 

例如，假設傾斜檢測所需的分辨率為1°，則±0.5°的誤差是可以接受的，因為它低于計算的舍入誤差。若在k = 1的情況下繪制實際傾角與計算傾角之間的誤差(如圖6所示)，則線性近似的有效范圍僅為±20°。若比例系數(shù)經調節(jié)后，使得誤差最大但依然保持在計算得到的舍入限值內，則線性近似的有效范圍增加到±30°以外。

 

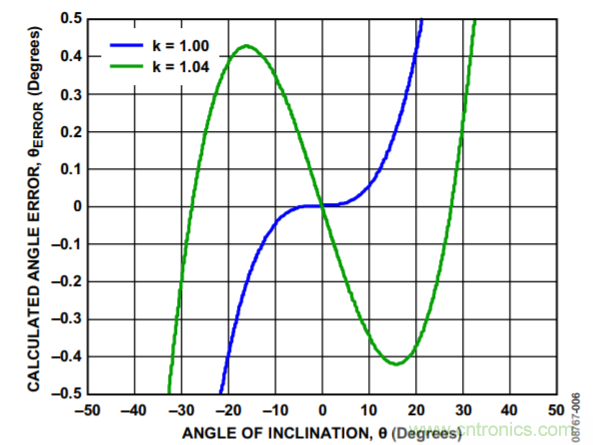
圖6. 不同比例系數(shù)下計算得到的角度誤差

 

雙軸傾斜計算

 

單軸傾斜檢測的一個限制，是需要高分辨率ADC或數(shù)字輸出來實現(xiàn)大范圍的有效傾角，如圖3和圖4所示；另一個限制，是單軸測量無法提供360°的測量，因為在傾角N°時產生的加速度與傾角180° − N°時產生的加速度相同。在某些應用中，這是可以接受的；但對于需要更高分辨率或要求在完整的360°弧度范圍內區(qū)分傾角的應用而言，則需要第二條軸(如圖7所示)，或者需要第二個傳感器。若使用了第二個傳感器，則其朝向應使第二個傳感器的檢測軸與第一個傳感器的檢測軸相互正交。

 

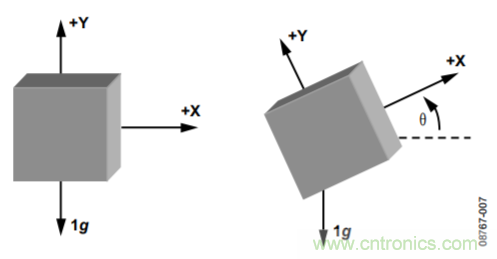
圖7. 用于傾斜檢測的雙軸

 

增加一個軸對確定傾斜角有三大好處。下文說明這些好處。

 

恒定靈敏度

 

增加一個軸的第一大好處在于兩個軸相互垂直。與單軸解決方案相同，x軸檢測到的加速度與傾斜角的正弦值成比例。由于兩個軸相互垂直，因此y軸加速度與傾斜角的余弦值成比例(見圖8)。隨著一條軸的增量靈敏度下降(比如該軸的加速度接近+1 g或−1 g)，另一條軸上的增量靈敏度將會上升。

 

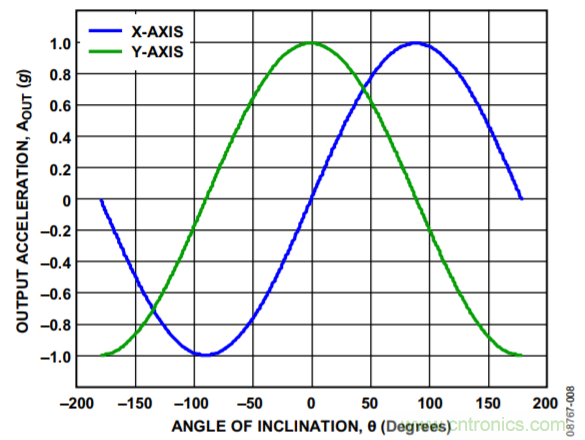
圖8. 輸出加速度與傾角的關系(雙軸傾斜檢測)

 

將測量的加速度轉換為傾角的一種方法，是計算x軸的反正弦函數(shù)和y軸的反余弦函數(shù)，與單軸解決方案類似。但是，更簡單有效的方法是使用兩個數(shù)值之比，可得到如下結果：

 

 

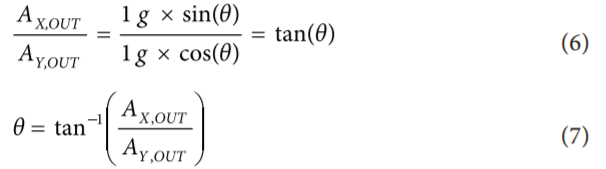
其中，傾斜角θ單位為弧度。

 

與單軸示例不同，使用兩軸之比來確定傾角會使得增量靈敏度的確定變得十分困難。相反，假設所需的傾斜分辨率已知，則確定加速度計需達到的最低分辨率用處更大。假定一條軸的增量靈敏度隨著另一條軸的增量靈敏度下降而上升，則凈結果將是數(shù)值基本恒定的有效增量靈敏度。這表示若針對某一角度，為達到所需的傾斜步長要求而選擇加速度計，則該加速度計將具備足夠的分辨率以應付所有角度。

 

為確定所需的最小加速度計分辨率，可檢查等式6，確定分辨率的極限。由于每條軸的輸出和傾角的正弦或余弦有關，并且每種函數(shù)的傾角均相同，因此可求解的最小角度與可求解的最小加速度有關。

 

如圖3和圖4所示，正弦函數(shù)在0°附近具有最大速率變化，且可以看出，余弦函數(shù)在該點處具有最小速率變化。由于這個原因，傾斜導致的x軸加速度變化將先于y軸加速度變化而被識別。因此，系統(tǒng)在0°附近的分辨率主要取決于x軸的分辨率。如需確定P°的傾斜變化，加速度計必須要能檢測根據(jù)下式所確定的變化量近似值：

 

 

對于所需的傾斜步長，圖9可用來確定所需的最小加速度計分辨率(或最大加速度計比例因子)。注意，加速度計分辨率的提升不僅與加速度計比例因子的降低有關，還與檢測更小的輸出加速度變化的能力有關。因此，針對目標傾斜步長選擇具有適當分辨率的加速度計時，比例因子應當小于圖9所示的限值。

 

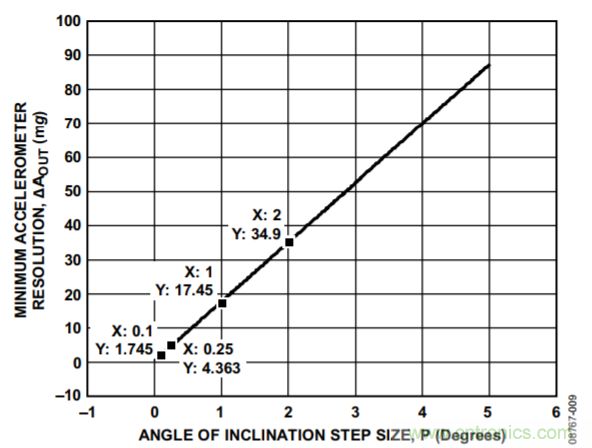
圖9. 用于目標傾角分辨率的最小加速度計分辨率

 

降低與重力平面對齊的依賴性

 

使用至少兩個軸的第二大好處是，與單軸解決方案不同，增加一個軸后，即使第三個軸上存在傾斜，也可以測出精確值。而在單軸解決方案中，只要除x軸以外的任何其它軸上存在傾斜，就會造成顯著誤差。這是因為有效增量靈敏度與目標軸上重力的和方根(RSS)值成比例。

 

若重力完全包含在xy平面中，那么在理想情況下，那些軸上檢測到的加速度RSS值等于1 g。若在xz或yz平面上存在傾斜，則重力導致的總加速度將下降，從而降低有效增量靈敏度。這樣會增加給定加速度計分辨率的傾斜步長，但依然可以提供精確的測量結果。傾角計算結果與xy平面上的旋轉有關。

 

若系統(tǒng)足夠傾斜，以至于xy平面上只有極少量由于重力而造成的加速度，那么傾角步長將會分辨率過低而不可用；因此，建議限制xz或yz平面的傾斜程度。

 

完整360°傾斜檢測

 

增加一個軸的第三大好處是，能夠區(qū)分各個象限并在整個360°弧度范圍內測量角度。如圖10所示，每個象限都具有與x和y軸加速度關聯(lián)的不同符號組合。

 

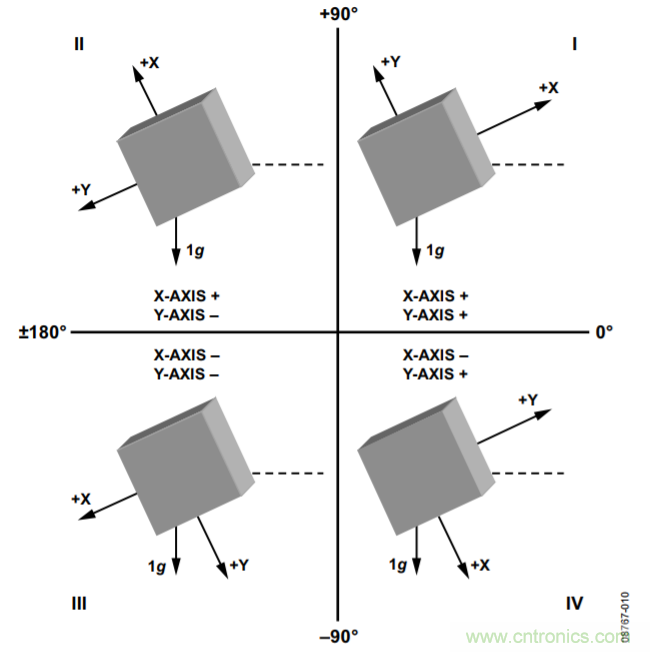
圖10. 象限檢測的傾角和加速度符號

 

如果操作數(shù)AX,OUT/AY,OUT為正值，反正切函數(shù)會返回第一象限中的值；如果操作數(shù)為負值，則反正切函數(shù)會返回第四象限中的值。第二象限內的操作數(shù)為負值，因此在計算該象限內的角度時應將結果加上180°。第三象限內的操作數(shù)為正值，因此在計算該象限內的角度時應從結果中減去180°。而該角度所處的確切象限則可以通過各軸上測得的加速度符號來確定。

 

三軸傾斜計算

 

引入第三條軸后，便可在全部范圍內確定傳感器。經典的矩形(x, y, z)到球形(ρ, θ, φ)轉換方法可將xy平面的傾角θ以及重力因素產生的傾角φ與每條軸上的測量加速度相關聯(lián)，如下所示：

 

 

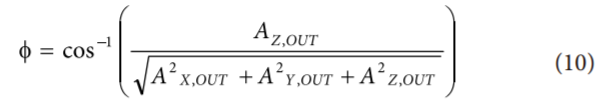
假設重力是唯一測得的加速度原因，則等式10分母上的操作數(shù)可以常數(shù)代替(最好是1)，因為此時所有軸上的RSS值為常數(shù)。角度如圖11所示；圖11c顯示θ只在xy平面上存在，而圖11d顯示φ為z軸與重力矢量之間的夾角。

 

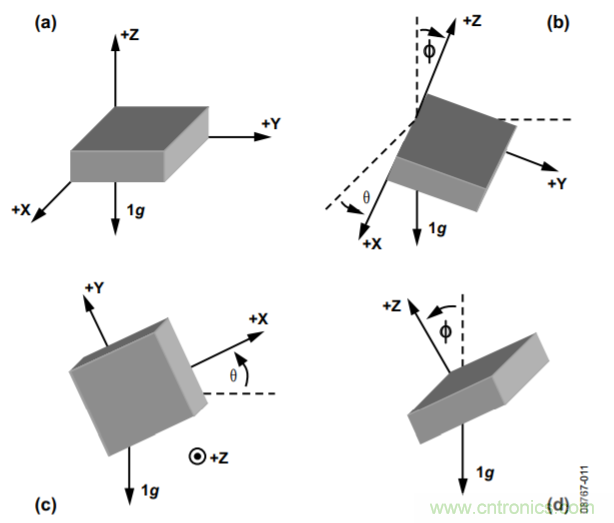
圖11. 球形坐標系統(tǒng)的角度

 

由于三軸法與單軸/雙軸法具有相似的等式，因此三軸解決方案的分析與單軸和雙軸法結合使用時相同。兩條正交軸之比有助于θ的測量，并且要達到要求的傾斜分辨率需要具備一個最小加速度計分辨率，如等式8所示。

 

φ的測量不僅與單軸解決方案的傾角測量有關，還與目標范圍內實現(xiàn)特定傾角分辨率所需的最小加速度計分辨率的確定有關。區(qū)別在于，使用反余弦函數(shù)確定φ會使φ在90°時具有最大的增量靈敏度，而在0°和180°時具有最小的增量靈敏度。

 

以余弦代替等式2中的正弦，即可產生類似圖3和圖4的曲線。重要的是需注意，雖然θ的范圍為−180°至+180°，但φ的范圍僅為0°至180°。若φ的角度為負數(shù)，則θ的角度也會變?yōu)樨摂?shù)。

 

三軸傾斜檢測的一種替代方法是單獨確定加速度計每條軸與參考位置之間的夾角。參考位置通常選擇器件的x軸和y軸位于水平面的方向上(0 g場)，并且z軸與水平面垂直(1 g場)。圖12顯示該方法，其中，θ表示水平面與加速度計x軸之間的夾角，ψ表示水平面與加速度計y軸之間的夾角，φ表示重力矢量與z軸之間的夾角。當位于x和y軸的0 g以及z軸的1 g初始位置時，所有計算的角度均為0°。

 

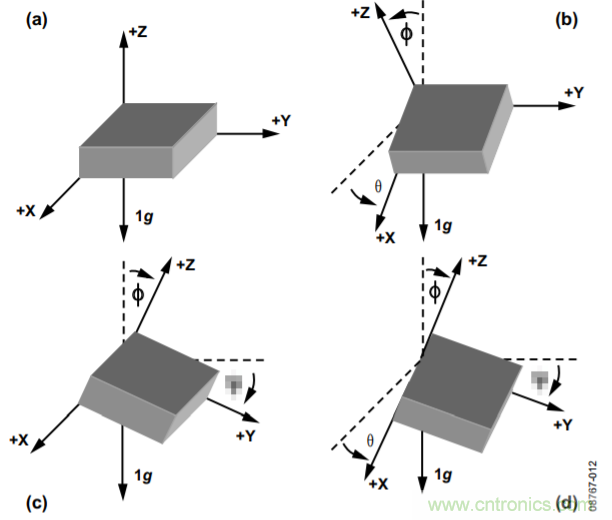
圖12. 獨立傾斜檢測的角度

 

可利用基本三角恒等式計算傾角，如等式11、12和13所示。

 

 

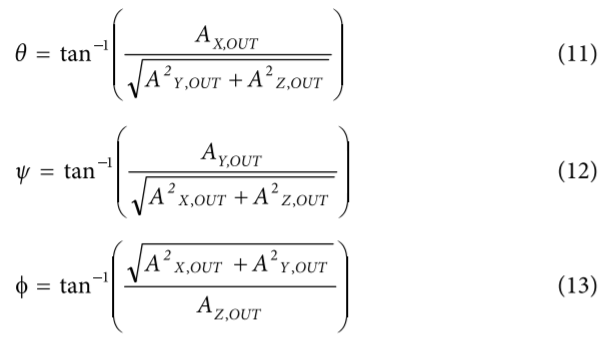
等式13中操作數(shù)出現(xiàn)明顯反轉，這是因為初始位置為1 g場。若需使用水平面作為z軸的參照，則可將操作數(shù)反轉。角度為正表示對應的加速度計正軸指向水平面上方，而角度為負表示軸指向水平面下方。

 

由于采用反正切函數(shù)和加速度之比，因此具有雙軸示例中提及的優(yōu)勢，也就是說有效增量靈敏度是恒定的，并且單位范圍內的角度可在所有點上精確測得。

 

校準失調和靈敏度失配誤差

 

本應用筆記中的分析假設采用理想加速度計。該假設等同于使用無0 g失調且具有完美靈敏度的器件——靈敏度以mV/g(模擬傳感器)或LSB/g(數(shù)字傳感器)表示。雖然傳感器經過調節(jié)，但器件本質上是機械的，這便意味著系統(tǒng)完成裝配后，器件上的任何靜態(tài)應力都有可能影響失調和靈敏度。再加上工廠校準的限制，便有可能使誤差超出應用允許的限值以外。

 

失調誤差的影響

 

為了表明誤差到底有多大，可以設想一下，某個雙軸解決方案具有完美的靈敏度，但x軸上存在50 mg失調。0°時，x軸讀數(shù)為50 mg，y軸讀數(shù)則為1 g。由此計算得出的角度就是2.9°，因而會造成2.9°的誤差。±180°時，x軸的讀數(shù)為50 mg，y軸的讀數(shù)則為−1 g。由此計算得出的角度會存在−2.9°的誤差。圖13所示為本例中算出的角度和實際角度之間的誤差情況。失調引起的誤差可能不僅大于系統(tǒng)所需的精度，而且還會發(fā)生變化，使簡單地通過校準消除誤差角變得困難。當多個軸上都存在失調時，這將會變得更為復雜。

 

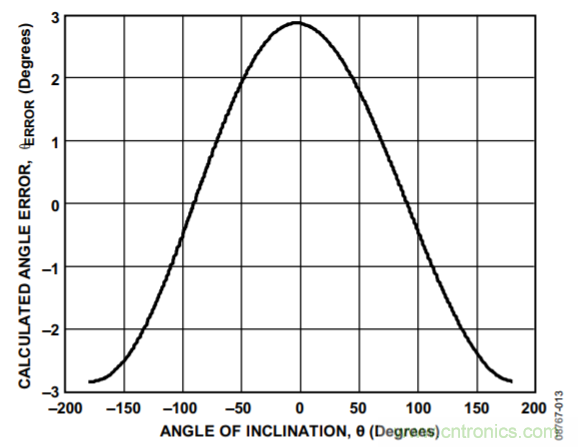
圖13. 加速度計失調引起的角度計算誤差

 

靈敏度失配誤差的影響

 

在雙軸傾斜檢測應用中，由加速度計靈敏度導致的主要誤差成分是目標軸之間的靈敏度差異(在單軸解決方案中，如果實際靈敏度和預期靈敏度之間存在任何偏差，則會導致出現(xiàn)誤差)。由于使用的是x和y軸的比值，因此如果兩者靈敏度相同，則可以消除大多數(shù)誤差。

 

下面舉例說明加速度計靈敏度失配的影響。假設某個雙軸解決方案具有完美的失調調整功能，且y軸具有完美的靈敏度，但x軸的靈敏度為+5%。這表示在1 g場中，y軸讀數(shù)為1 g，x軸讀數(shù)則為1.05 g。圖14所示為因為這種靈敏度失配而造成角度計算出現(xiàn)的誤差情況。與失調誤差類似，加速度計靈敏度失配引起的誤差會在整個旋轉范圍內不斷變化，使在計算出傾斜角后進行誤差補償變得困難。改變y軸的靈敏度會進一步增加失配，從而使誤差更大。

 

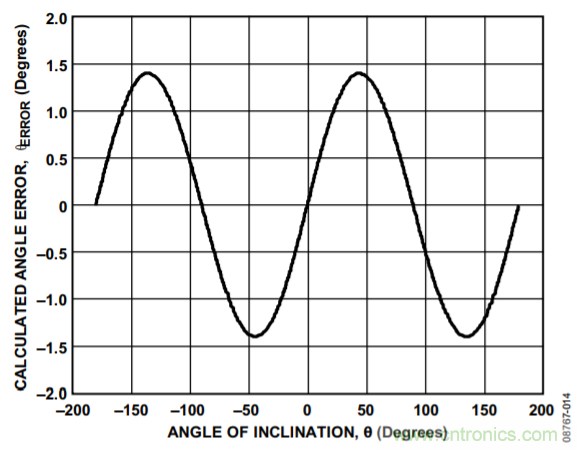
圖14. 加速度計靈敏度失配引起的角度計算誤差

 

基本校準技術

 

當失調引起的誤差和靈敏度失配引起的誤差兩者相疊加時，誤差可能會變得相當大，完全超出傾斜檢測應用所能接受的范圍。要減少這類誤差，就應當對失調和靈敏度進行校準，并使用校準后的輸出加速度來計算傾斜角。包括失調和靈敏度的影響后，加速度計輸出變化如下：

 

 

其中：

 

AOFF表示失調誤差，單位為g。

 

Gain表示加速度計的增益，理想值為1。

 

AACTUAL表示加速度計的真實加速度和目標值，單位為g。

 

一種簡單的校準方法是假設增益為1并測量失調。經過此校準之后，系統(tǒng)的精度即會限制為未校準的靈敏度誤差。這種簡單的校準方法可通過將目標軸置于0 g場中并測量輸出(大小等于失調)來完成。然后，應在處理信號之前從加速度計的輸出中減去該值。這種方法通常稱為無調頭或單點校準，因為器件的典型取向會將x和y軸置于0 g場中。如果使用的是三軸器件，則應針對z軸包含至少一個調頭或第二個點。

 

一種更加精確的校準方法是每個目標軸上取用兩個點(三軸設計最多可取用六個點)。當某個軸處于+1 g和−1 g場中時，測得的輸出如下：

 

 

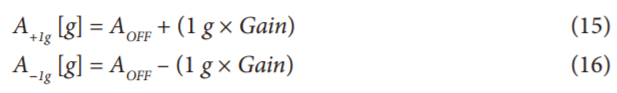
其中，失調AOFF的單位為g。

 

利用這兩個點確定的失調和增益如下：

 

 

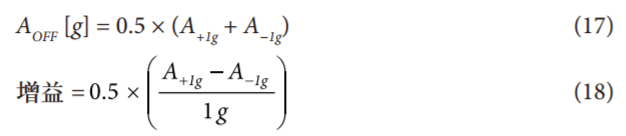
其中，+1 g和−1 g測量結果A+1g和A−1g均以g表示。

 

由于測量目標軸時，正交軸都處于0 g場，因此這種校準方法還有助于將跨軸靈敏度影響降至最低。利用這些值，首先可以從加速度計測量結果中減去失調，然后將所得結果除以增益。

 

 

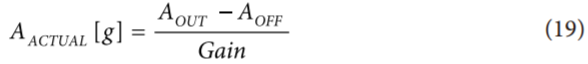
其中，AOUT和AOFF的單位為g。

 

等式15至等式19中，計算AOFF和增益時，假設加速度值A+1g和A−1g均以g表示。如果加速度單位采用mg，則等式17中AOFF的計算結果會保持不變，但等式18中增益的計算結果需要除以1000，以處理單位上的變化。

 

 

推薦閱讀：