【導(dǎo)讀】本文詳解控制理論。通常我們?cè)谥v解控制理論時(shí),都只通過框圖,而不參考實(shí)際的電路。在數(shù)學(xué)和電路仿真工具的幫助下,我們將一步步說明電子控制理論與現(xiàn)代電路設(shè)計(jì)息息相關(guān)。
簡(jiǎn)介
大學(xué)教授的許多科目都會(huì)令學(xué)生發(fā)問:"學(xué)習(xí)這門課程能讓我找到一份工作嗎?"控制理論可能就是這樣一門課程,這些多達(dá)數(shù)頁(yè)的數(shù)學(xué)和框圖不會(huì)在實(shí)際電路中被直接使用。但是,控制系統(tǒng)教授工程師如何設(shè)計(jì)自動(dòng)系統(tǒng)、系統(tǒng)距離實(shí)現(xiàn)穩(wěn)定操作還有多大距離,以及如何從給定系統(tǒng)獲得最佳響應(yīng)。因?yàn)椴还苷n程是關(guān)于機(jī)械、電氣、土木、航空,或者是通信工程,如果系統(tǒng)不穩(wěn)定,一切都沒有用。
對(duì)于設(shè)計(jì)工程師來說,控制理論就是生命本身。
現(xiàn)在有許多關(guān)于控制理論的優(yōu)秀文章,但是其中很多都是借助框圖,以最概括化的方法來進(jìn)行介紹。本文主要面向電子工程師,從電路分析和仿真的角度介紹電子控制系統(tǒng);介紹了常見的二階系統(tǒng)背后的理論,而且是利用有效的電路示例來加以說明;旨在揭露二階系統(tǒng)的基礎(chǔ)原理,并向嘗試了解電子控制理論的人員說明,該理論與模擬電路設(shè)計(jì)之間存在關(guān)聯(lián)。
二階系統(tǒng)
圖1所示為最基礎(chǔ)的二階網(wǎng)絡(luò)。
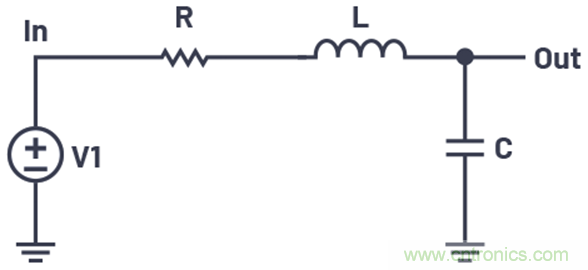
圖1.由一個(gè)電阻、一個(gè)電感和一個(gè)電容構(gòu)成的二階網(wǎng)絡(luò)。
其傳遞函數(shù)為:

方程1右側(cè)的分母被稱為 特征多項(xiàng)式 ,如果我們令特征多項(xiàng)式為0,我們會(huì)得出 特性方程。當(dāng)轉(zhuǎn)換函數(shù)的分母等于0時(shí),得到系統(tǒng)的極點(diǎn) 通過求解特性方程的根(讓特性方程等于0的s的值),我們可以找到系統(tǒng)的極點(diǎn),從而獲取與系統(tǒng)運(yùn)行狀況相關(guān)的許多信息。
二階系統(tǒng)傳遞函數(shù)的一般形式為:
其中ζ表示阻尼系數(shù),ωn表示電路的固有振蕩頻率(或無阻尼頻率),單位為弧度/秒。
所以,二階系統(tǒng)的一般特性方程為:
比較方程3和方程1,我們可以看出,圖1中的電路的固有頻率為:
我們也可以看出,電路中的電阻會(huì)影響網(wǎng)絡(luò)的阻尼系數(shù):
所以
所以
可以直觀看出,如果電路中沒有電阻,網(wǎng)絡(luò)不會(huì)出現(xiàn)耗損(無阻尼),如果模擬這種電路,則電路會(huì)永久振蕩。隨著電阻增加,振蕩會(huì)更快衰減。
圖2顯示一個(gè)RLC電路,其中階躍輸入為1 V,L = 1 µH,C = 1 µF,電阻分別為0 Ω、100 mΩ和500 mΩ。電路按照預(yù)期的159 kHz頻率振蕩。電阻增加對(duì)衰減的影響一目了然。
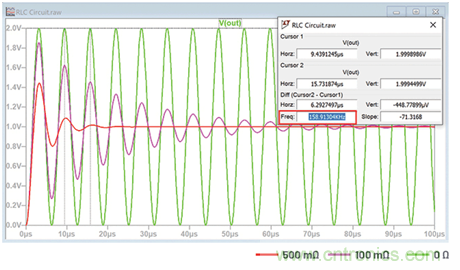
圖2.電阻對(duì)網(wǎng)絡(luò)振蕩的衰減影響。
我們可以通過將拉普拉斯域轉(zhuǎn)換為時(shí)域,以數(shù)學(xué)方式展示圖2所示的模擬結(jié)果。拉普拉斯域中的單位階躍輸入寫為:
所以當(dāng)我們使用單位階躍輸入仿真二階系統(tǒng)時(shí),結(jié)果會(huì)變成:
如果使用部份分式分解法,方程9可以寫為:
方程10是表示在拉普拉斯域中的。
在時(shí)域中,這會(huì)轉(zhuǎn)換為:
其中
采用逆拉普拉斯變換的公式11的數(shù)學(xué)推導(dǎo)如 附錄A所示。
通過公式11,我們可以看出圖1的電路如何響應(yīng)階躍輸入。我們可以看到,波形具有與正弦曲線類似的特性,其幅度則由e–ζωnt項(xiàng)調(diào)制,根據(jù)阻尼系數(shù)是正數(shù)或復(fù)數(shù)出現(xiàn)指數(shù)式衰減或增加。近似來看,響應(yīng)由正弦部分和余弦部分組成,但是,阻尼系統(tǒng)較低時(shí),正弦部分非常小。
此外,盡管電路的固有頻率為ωn,但電路不會(huì)按照此頻率振蕩,而是按照更低一些的頻率ωdn決定。
要找出轉(zhuǎn)換函數(shù)的極點(diǎn),則需要確定轉(zhuǎn)換函數(shù)何時(shí)等于0,也就是說:
s的值可以使用二次方程求解:
其中
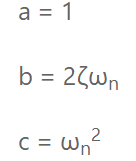
要得出系統(tǒng)極點(diǎn),需要:
如果阻尼系數(shù)小于1,會(huì)得出負(fù)的平方根,所以最好將方程15寫作:
我們之前說過 ωd = ωn√(1 – ζ2),所以方程16可以改寫為:
這里我們可以看出,系統(tǒng)的極點(diǎn)包含實(shí)數(shù)部分(–ζωn) 和虛數(shù)部分 (±jωd)。
方程17可以求解得出特性方程的根(系統(tǒng)的極點(diǎn))。我們?nèi)绾螌⑦@些極點(diǎn)與系統(tǒng)的穩(wěn)定性聯(lián)系起來?現(xiàn)在我們需要把拉普拉斯域的極點(diǎn)和時(shí)域的穩(wěn)定性聯(lián)系起來。
通過方程11和方程17,我們可以得出以下觀察結(jié)果。
無阻尼固有頻率ωn決定了:
拉普拉斯域(方程17)中的極點(diǎn) (–ζωn)的虛數(shù)部分。
振蕩的實(shí)際頻率
由此,可以合理假設(shè)極點(diǎn)的虛數(shù)部分確定了系統(tǒng)振蕩的實(shí)際頻率。
這兩個(gè)假設(shè)可以用s平面圖表示,我將在下一節(jié)詳細(xì)介紹。
穩(wěn)定的系統(tǒng)
控制理論認(rèn)為,如果極點(diǎn)位于s平面的左半部分,則系統(tǒng)是穩(wěn)定的。圖3所示為一個(gè)s平面示例,其中實(shí)數(shù)部分在x軸上繪制,虛數(shù)部分在y軸上繪制。
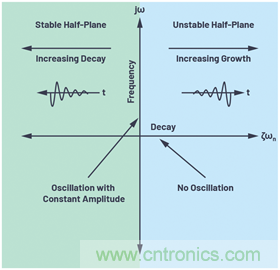
圖3.s平面:顯示穩(wěn)定的左半部分和不穩(wěn)定的右半部分。
從方程17可以看出,如果阻尼系數(shù)為正(方程17的實(shí)數(shù)部分為負(fù)),則極點(diǎn)位于左半部分。隨著阻尼系數(shù)增加,方程17的極點(diǎn)進(jìn)一步向左移動(dòng)(在左側(cè)平面內(nèi),越來越靠近左側(cè))。
如果方程17在拉普拉斯域中,如何在時(shí)域中轉(zhuǎn)換?
為了方便起見,我們?cè)俅问褂梅匠?1:
正阻尼系數(shù)ζ會(huì)引發(fā)指數(shù)式的衰減幅度響應(yīng)(由e–ζωnt項(xiàng)表示),阻尼越大,衰減越快。隨著阻尼系數(shù)增加,極點(diǎn)進(jìn)一步向左移動(dòng)(在拉普拉斯域內(nèi)),這進(jìn)一步增大了時(shí)域內(nèi)的指數(shù)式衰減。從圖2中可以看出這一點(diǎn),圖2使用100 mΩ和500 mΩ線路來表述電阻對(duì)阻尼的影響。在此區(qū)域中,500 mΩ線路的阻尼系數(shù)最大,所以它的指數(shù)式衰減最明顯。0 Ω時(shí),阻尼系數(shù)為0,此時(shí)極點(diǎn)完全位于y軸上,電路無限振蕩,如圖2中的綠色線路所示。
值得注意的是,即使系統(tǒng)是穩(wěn)定的,這并不表示一定沒有振蕩。電路可能會(huì)在左半平面的極點(diǎn)處振蕩,但是這些振蕩的振幅會(huì)隨著時(shí)間而衰減,如圖2所示。
這對(duì)圖1中的電路意味著什么?
我們知道圖1中的阻尼是通過下方的方程得出:
它的固有頻率則是:
所以,在L = 1 µH,C = 1 µF時(shí),固有頻率為1 Mrads–1 (= 159.1 Hz),R = 500 mΩ時(shí)的阻尼系數(shù)為0.25。
所以,阻尼振蕩頻率ωd由以下方程計(jì)算得出:
所以,阻尼振蕩頻率為968 krads–1,即154 kHz。這可以通過查看圖4中紅色波形的頻率來說明。
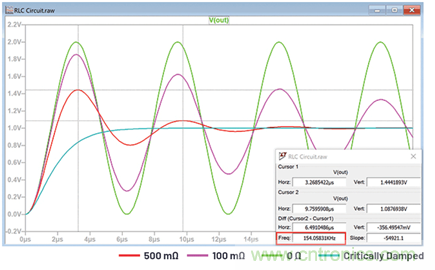
圖4.阻尼對(duì)RLC電路振幅和頻率的影響。
正弦波的振幅按e–ζωnt衰減。阻尼系數(shù)為0.25,固有頻率ωn為1 Mrads–1,阻尼固有頻率為968246 rads–1,那么方程11變成:
使用這個(gè)公式,計(jì)算得出VOUT在3.26 μs時(shí)為1.44 V,在9.75 μs時(shí)為1.09 V,與圖4中顯示的讀數(shù)完全一致。
圖4清楚顯示了增加阻尼系數(shù)會(huì)產(chǎn)生的影響,即振幅和阻尼固有頻率都減小。
如果我們繼續(xù)增大阻尼系數(shù),會(huì)出現(xiàn)什么結(jié)果?
我們知道阻尼固有頻率是通過以下方程計(jì)算得出:
當(dāng)阻尼系數(shù)增大到一時(shí),阻尼固有頻率減小到零。這就是所謂的臨界阻尼點(diǎn),此時(shí)電路中的所有振蕩終止。這一點(diǎn)可參見方程11。自阻尼固有頻率ωd減小到0,正弦項(xiàng)等于0,余弦項(xiàng)目等于一,表達(dá)式簡(jiǎn)化為一階系統(tǒng),與通過電阻充電的電容完全一樣。
這一點(diǎn)可以參見圖4中的臨界阻尼線路。
不穩(wěn)定系統(tǒng)
由于所有電路都具有電阻,所以許多電子控制電路的極點(diǎn)都位于左半平面,且系統(tǒng)本身保持穩(wěn)定。但是,由方程11可以看出,負(fù)阻尼系數(shù)會(huì)導(dǎo)致振幅響應(yīng)呈指數(shù)增長(zhǎng),所以極點(diǎn)位于右半平面會(huì)導(dǎo)致系統(tǒng)不穩(wěn)定。在電路模擬中,通過插入負(fù)電阻,可以很容易看出右半平面的影響。圖5顯示RLC電路,其電阻為負(fù)。
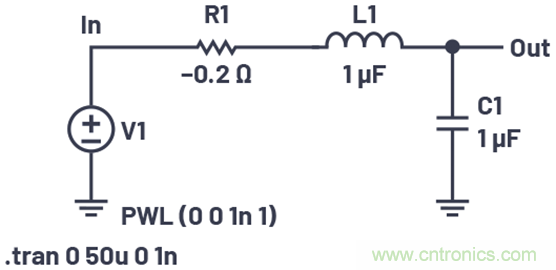
圖5.電阻為負(fù)的RLC電路。
該電路的阻尼系數(shù)為-0.1。圖6顯示了它對(duì)階躍輸入的響應(yīng)。

圖6.阻尼為負(fù)的二階系統(tǒng)的階躍響應(yīng)。
阻尼固有頻率仍然由以下方程表示:
阻尼系數(shù)為-0.1時(shí),振蕩的實(shí)際頻率為994987 rads–1 (158.3 kHz)。
同樣,從方程11可以看出電路響應(yīng)由以下公式表示:
在輸出增大時(shí),我們可以得出振幅響應(yīng):VOUT在41.05 μs時(shí),計(jì)算得出的值為61.62 V,在47.36 μs時(shí),為114.99 V,與圖6中所示的讀數(shù)完全一致。
主導(dǎo)極點(diǎn)
有時(shí)一個(gè)系統(tǒng)由許多極點(diǎn)組成,使分析變得復(fù)雜。但是,如果極點(diǎn)之間相隔的距離足夠大,那么一個(gè)極點(diǎn)產(chǎn)生的影響會(huì)占主導(dǎo),因此可以忽略非主導(dǎo)極點(diǎn),從而簡(jiǎn)化系統(tǒng)。
圖7的上半部分顯示了兩個(gè)RLC電路,每個(gè)都使用完全相同的L和C元件;只是電阻發(fā)生了變化。電阻較低的電路的極點(diǎn)更靠近s平面的虛數(shù)軸。
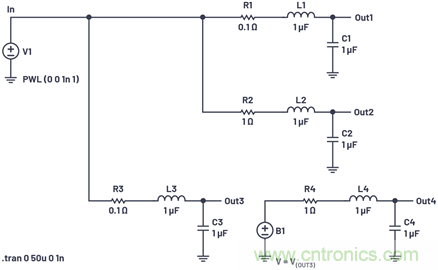
圖7.主導(dǎo)極點(diǎn)的位置對(duì)串聯(lián)和并聯(lián)電路的影響。
圖7的下半部分顯示了這兩個(gè)電路的串聯(lián)。我們使用行為電壓源B1來復(fù)制V(OUT3),以免它被R4、L4和C4加載,以便我們查看V(OUT3) × V(OUT4)的真實(shí)響應(yīng)。
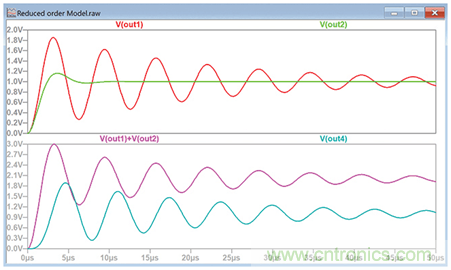
圖8.當(dāng)兩個(gè)波形相加或相乘時(shí),主導(dǎo)極點(diǎn)對(duì)系統(tǒng)響應(yīng)的影響。
我們可以參考圖8查看它們的響應(yīng)。不出所料,電阻最大的電路具有最大的阻尼系數(shù),因此其振蕩衰減也最快,如圖V(OUT2)所示。但是,我們注意到,當(dāng)兩個(gè)輸出要么相加(使電路并聯(lián)),要么相乘(使電路串聯(lián))時(shí),V(OUT1)在響應(yīng)中占主導(dǎo)。因此,要簡(jiǎn)化復(fù)雜的系統(tǒng),方法之一是重點(diǎn)關(guān)注極點(diǎn)更靠近jω軸的電路,該電路會(huì)主導(dǎo)整個(gè)系統(tǒng)的響應(yīng)。
在左右半面均有極點(diǎn)分布的系統(tǒng)
我們已經(jīng)考慮過極點(diǎn)位于左半平面或右半平面的系統(tǒng)。如果系統(tǒng)在左右半面均有極點(diǎn)分布,會(huì)怎么樣?哪一種在穩(wěn)定性方面更勝一籌?為什么?
我們?cè)俅螀⒖挤匠?1,可以看出指數(shù)是決定系統(tǒng)是否穩(wěn)定的決定因素。我們可以忽略方程11的正弦部分,只看指數(shù),以了解如果我們將左半面的極點(diǎn)和右半面的極點(diǎn)結(jié)合,會(huì)發(fā)生什么。圖9通過一個(gè)簡(jiǎn)單電路來進(jìn)行演示。
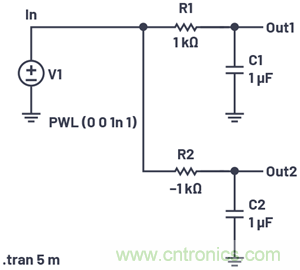
圖9.極點(diǎn)分別位于左半面和右半面的電路。
很顯然,頂部的RC電路的極點(diǎn)位于左半面,因?yàn)樗碾娮铻檎?。底部電路的極點(diǎn)則位于右半面。得出此結(jié)論的數(shù)學(xué)推導(dǎo)如 附錄B所示。
圖9中,電路的響應(yīng)如圖10所示。
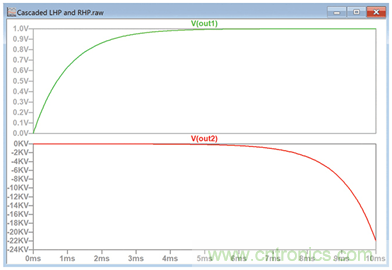
圖10.對(duì)具有正負(fù)電阻的RC電路的階躍輸入的響應(yīng)。
頂部波形在大約5毫秒后穩(wěn)定在零梯度,這符合大眾接受的規(guī)則,即RC電路將穩(wěn)定在大約5個(gè)時(shí)間常數(shù)。相反,V(OUT2)的梯度不斷增加。現(xiàn)在可以明顯看出,如果將極點(diǎn)位于左半面的電路和極點(diǎn)位于右半面的電路串聯(lián),那么整個(gè)電路會(huì)不穩(wěn)定,這是因?yàn)樵谧蟀朊骐娐贩€(wěn)定很長(zhǎng)時(shí)間后,右半面電路的響應(yīng)會(huì)繼續(xù)呈指數(shù)上升。因此,為了讓電路穩(wěn)定,所有極點(diǎn)都必須位于左半面。
結(jié)論
本文將電子控制理論中使用的理論模型與電子工程師所處的現(xiàn)實(shí)聯(lián)系起來。受系統(tǒng)中的電阻(或阻尼)影響,只有當(dāng)所有極點(diǎn)都位于左半面時(shí),控制系統(tǒng)才會(huì)保持穩(wěn)定。對(duì)于極點(diǎn)位于右半面的系統(tǒng),通過測(cè)量其輸出響應(yīng),結(jié)果證實(shí)存在問題,因?yàn)檫@需要構(gòu)建負(fù)電阻模型。幸好,計(jì)算機(jī)模擬幫我們解決了這個(gè)問題,讓我們能夠通過簡(jiǎn)單變更電阻的極性來展示穩(wěn)定和不穩(wěn)定的電路。
同樣,拉普拉斯變換也很少在課堂之外出現(xiàn),但在驗(yàn)證二階電子系統(tǒng)如何工作時(shí),它們的作用可謂是無價(jià)的。
附錄A
顯示
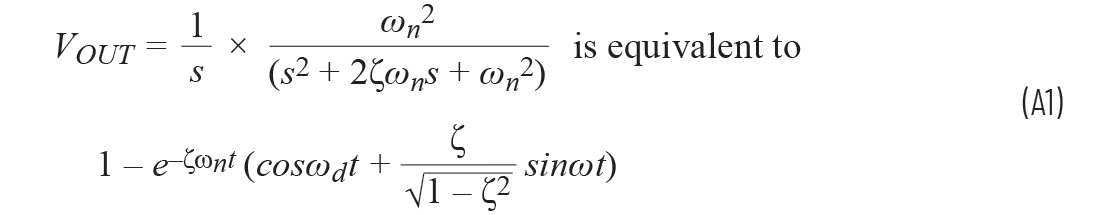
單位階躍輸入的拉普拉斯變換為
二階低通濾波器的通用轉(zhuǎn)換函數(shù)為
所以,由單位階躍模擬的二階系統(tǒng)的響應(yīng)為
使用了標(biāo)準(zhǔn)的部份分式分解法,方程如下:
用s代替x之后,
在A4中,分子中不含s或s2。而且,分母中也不含a。
所以方程A6可以改寫為
因此
為保證方程A8兩邊的分母相同,可以將其改寫為
為了驗(yàn)證,可以將方程A9的右側(cè)與方程A8的右側(cè)進(jìn)行比較:
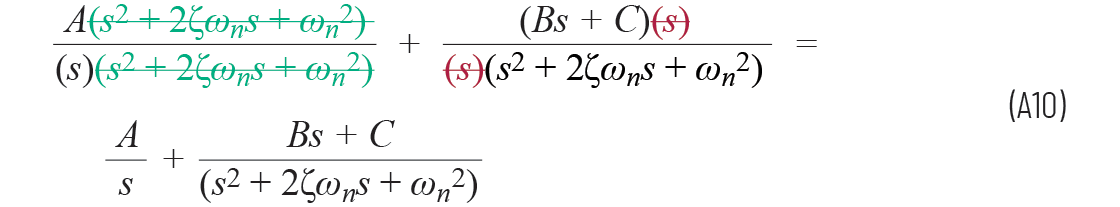
現(xiàn)在,我們可以使方程A9的分母相等,以求解A、B和C:
s2的系數(shù)相等:
0 = A + B
s1:的系數(shù)相等:
0 = A(2ζωn) + C
s0:的系數(shù)相等:
ωn 2 = Aωn 2
所以A = 1, B = –1, C = –2ζωn
因此,通過方程A8可以得出
(注意符號(hào)的變化,因?yàn)锽和C都為負(fù))
從時(shí)域(左邊)到拉普拉斯域(右邊)有三次變換:

通過完成平方計(jì)算,我們可以把方程A12寫為
等于
我們現(xiàn)在需要讓分子等于 (s + 2ζωn) ,使其與分母中的第一項(xiàng)匹配,以便我們使用拉普拉斯定義:
因此,通過將ζωn分子項(xiàng)分解為分式,方程A15等于
(所以, a = –ζωn b = ωn√(1 – ζ2))
我們現(xiàn)在需要讓方程A17的第三個(gè)項(xiàng)等于ωn√(1 – ζ2) ,使其和分母匹配,以便我們使用拉普拉斯定義:
用方程A17的第三個(gè)項(xiàng)除以 ωn√(1 – ζ2),然后將 ωn√(1 – ζ2)放在分子位置。
那么整個(gè)方程可以改寫為
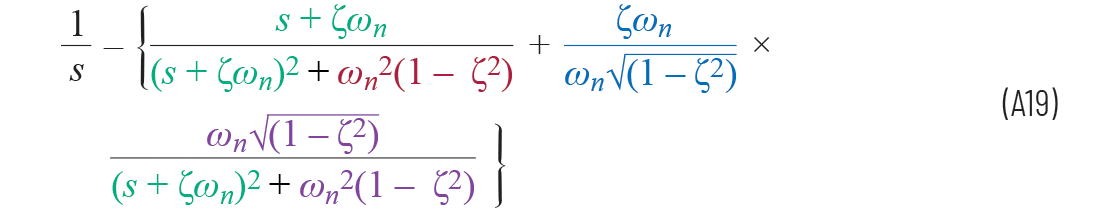
所以 a = –ζωn b = ωn√(1 – ζ2)
方程A19現(xiàn)在可以從拉普拉斯域中轉(zhuǎn)變?yōu)?/div>
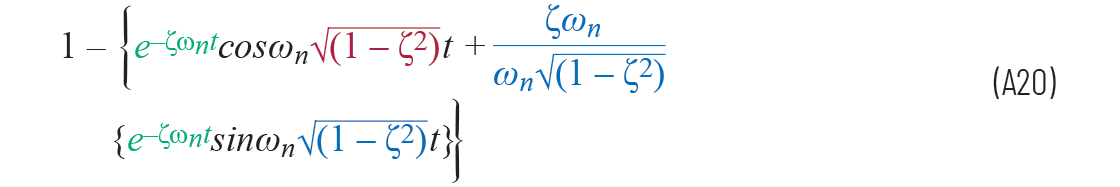

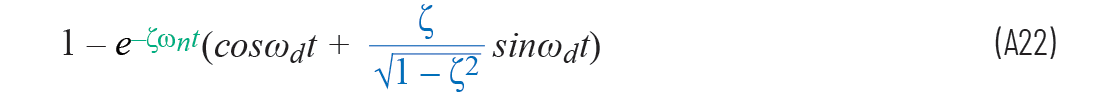
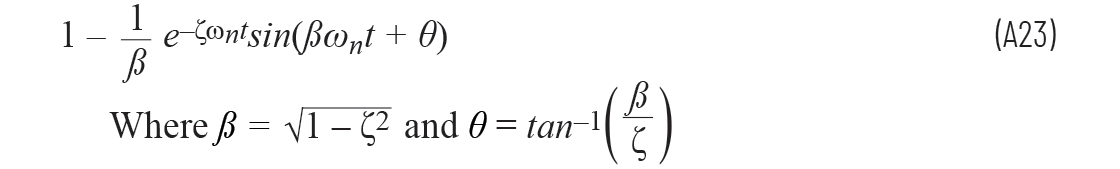
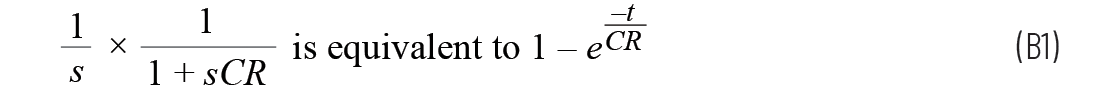


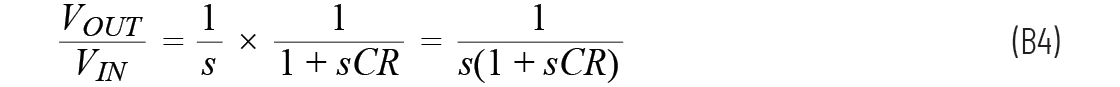
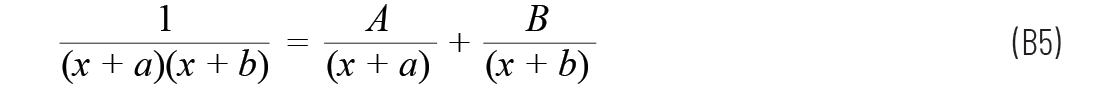
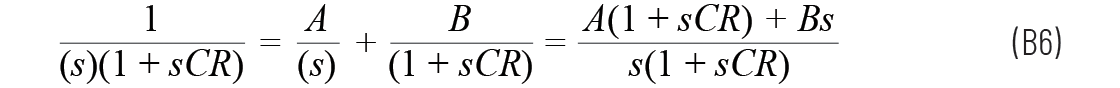
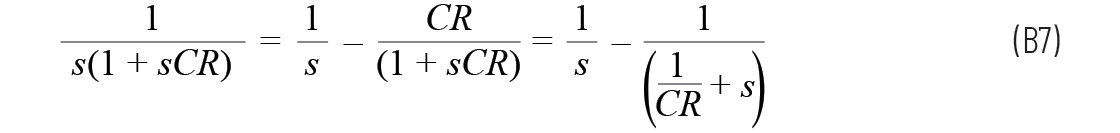


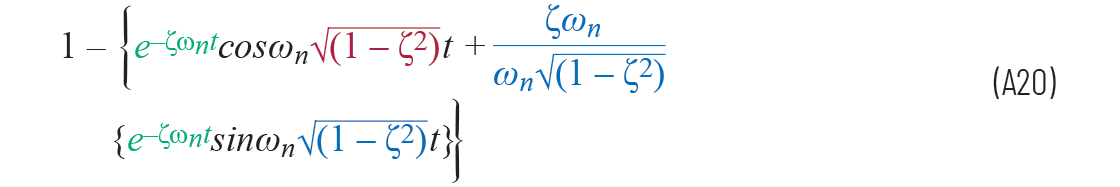
第三項(xiàng)中取消了兩個(gè)wn。因?yàn)樽枘峁逃蓄l率ωd可以寫為
方程A21可以簡(jiǎn)化為
許多課本中提到,方程A21的多項(xiàng)式也可以寫為
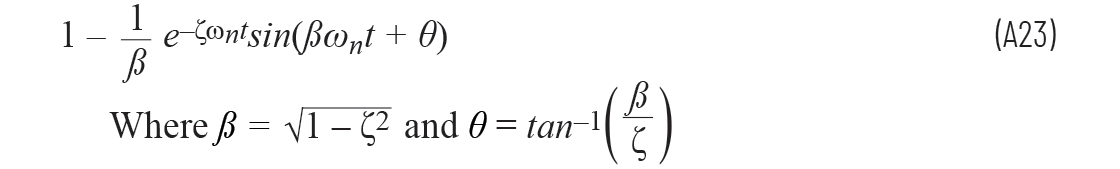
所以我們的衰減指數(shù)由阻尼系數(shù)和無阻尼固有頻率決定,振蕩由阻尼固有頻率決定。
可以將方程A23輸入電子表格和表示輸出與階躍輸入之間關(guān)系的圖表中。
附錄B
顯示
單位階躍輸入的拉普拉斯變換為
RC電路的通用轉(zhuǎn)換函數(shù)為:
s為負(fù)值時(shí),分母為零,所以這個(gè)電路的極點(diǎn)位于左半面上,因此系統(tǒng)是穩(wěn)定的。如果電阻為負(fù),那么極點(diǎn)位于右半面,系統(tǒng)會(huì)不穩(wěn)定。
從方程B3可以看出,RC電路的轉(zhuǎn)換函數(shù)與階躍輸入之間的關(guān)系為
使用了標(biāo)準(zhǔn)的部份分式法,方程如下:
在本例中,a = 0
所以
分子中s1 的相等項(xiàng)為
0 = ACR + B
分子中 s0的相等項(xiàng)為
1 = A
所以 A = 1, B = –CR
因此
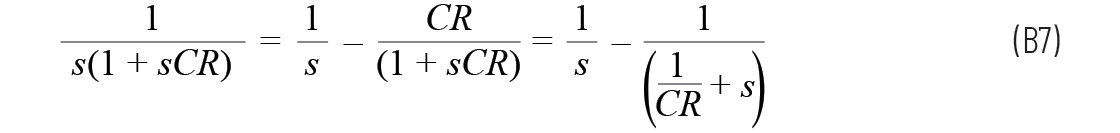
從時(shí)域(左邊)到拉普拉斯域(右邊)有兩次變換:

將方程B7轉(zhuǎn)化為采用時(shí)域意味著RC按照預(yù)期
進(jìn)行響應(yīng)。
附錄
下載與本文相關(guān)的 LTspice® files 文件。
欲了解有關(guān)LTspice的更多信息,請(qǐng)?jiān)L問analog.com/ltspice。
參考電路
Charles Phillips、Royce Harbor。《反饋控制系統(tǒng)》,第4版。Prentice Hall International,1988年。.
致謝
我們采用 LTspice進(jìn)行模擬。
非常感謝倫敦布魯內(nèi)爾大學(xué)的Maysam Abbod為本文實(shí)施理論校正。
推薦閱讀:







